Doing simulations of physics is another important constituent part of the experiments. I learned some basic rules of simulation in computational physics classes as well as waveguide, solid state physics and EMW related classes. Here are some examples.
Movements
我对运动的仿真并不是很在行,原因之一就是力学学得不好,导致有些模型不会分析。不用说分析力学的各种张量分析,就说简单的经典力学,六个自由度列方程我经常都列不对,更别说解方程了。因而,这一部分的仿真完全是参考[^1]这本书的第二章、第三章完成的。主要研究了常见的抛物运动附加各种阻力,例如炮弹、棒球、高尔夫球、足球等等。主要的一个影响因素就是Magnus Force,把它仿真好了基本就可以。
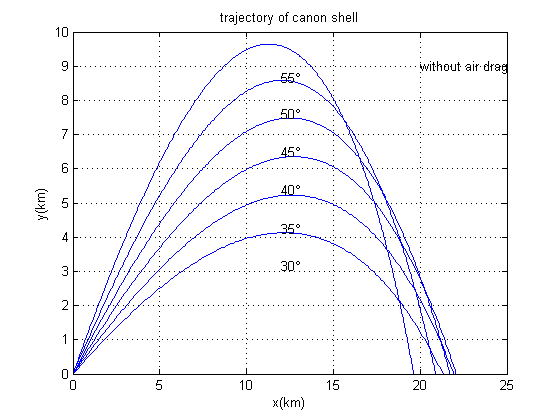
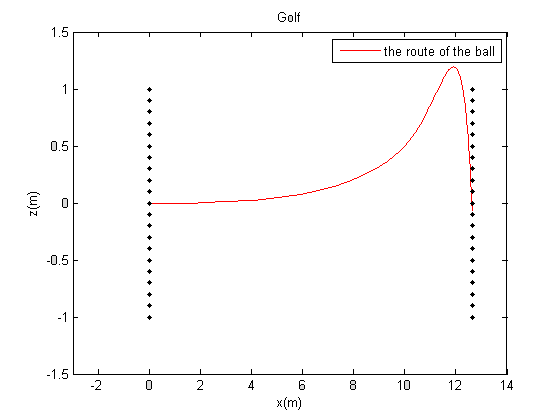
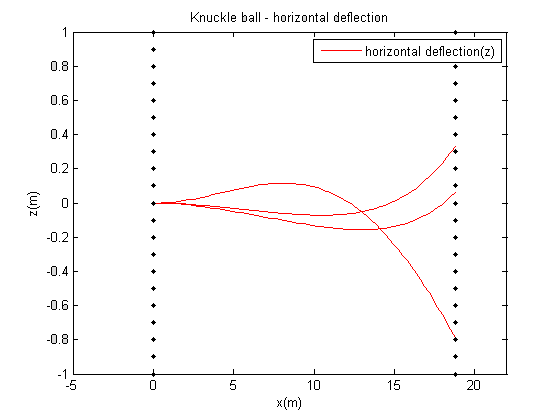
附图是上述三者的仿真。第一次做出knuckleball仿真时候还以为自己做错了,结果看到一个GIF发现现实比仿真还离谱……见下图

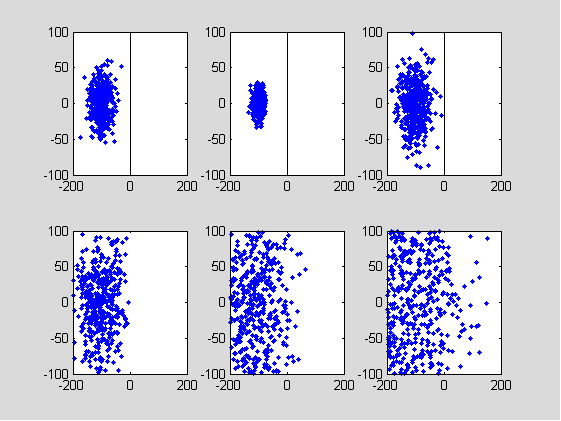
Oscillation and chaos
尽管做了许多关于混沌的仿真,但直到如今我对混沌也是一知半解。总体来说,混沌无非是在ODE方程组中引入了非线性项。简单的例如sin/cos、二阶三阶四阶项、指数项等等;复杂的比如取绝对值、限幅、其它的指数项等等……其实自己见得也不多,除了常见的那几种Logistic,Rossler之类的和蔡氏电路原始版的方程以外,基本也没研究过啥。不是特别感兴趣,感觉有些难……
周期性振荡是混沌的前体。首先找出各种振荡的方程组,从简谐振动出发:
\[\ddot x + {\omega ^2}x = 0\]
非常简单的一元二阶常微分方程。稍作改动,加上周期驱动力和非线性项,便会出现一些非线性的特征,例如:
\[\ddot x + q\dot x + \frac{g}{l}\sin x - {F_D}\sin \left( {\Omega _D}t \right) = 0\]
适当给定驱动力FD就能得到不同的相图。其中一个长这样:(是不是有点艺术感?)
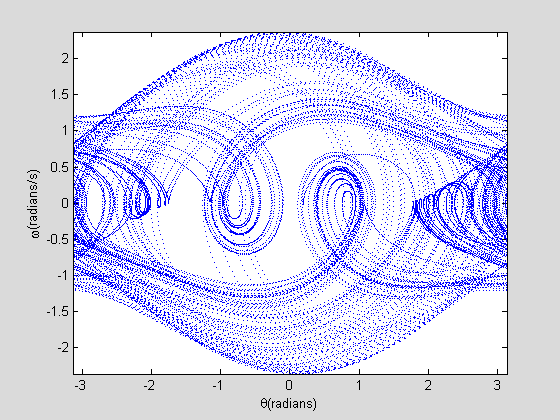
除了改变一阶项的形式以外,当然还可以将其变为多元方程组。常见的Rossler混沌就是三元一阶非线性方程组,通过元素之间的乘积引入非线性。相图是比较有特点的,过目难忘:
不得不提的是被与著名的“蝴蝶扇动翅膀引起德州龙卷风”说法紧密联系的洛伦兹振荡。洛伦兹作为气象学家从复杂的气象模型中提炼出经典的模型,这个相图也因此被命名为蝴蝶图,
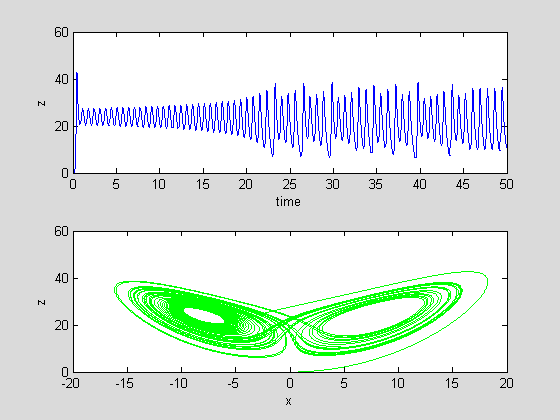
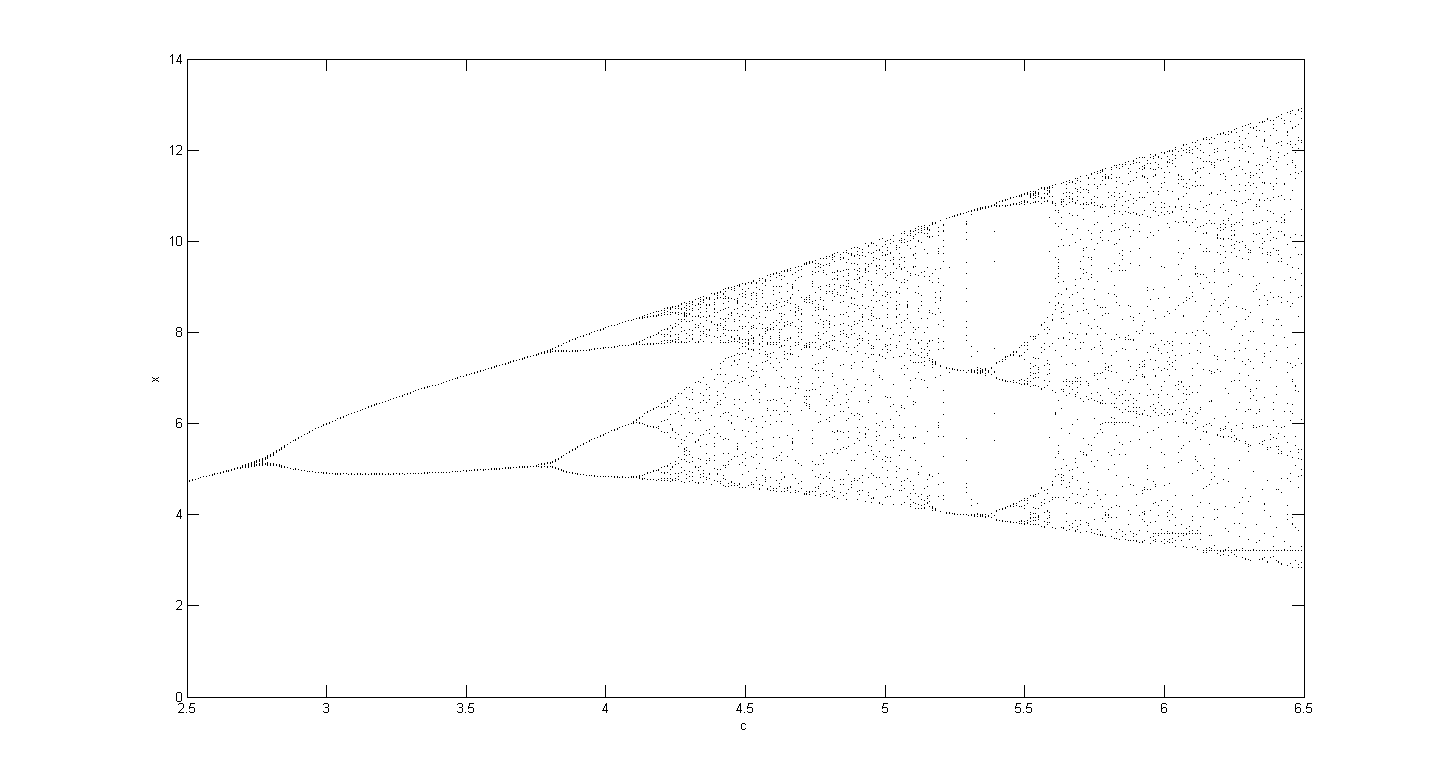
另外,迭代也是另一类形成混沌的方法。最简单的例如逻辑斯蒂映射:
\[x(t+1)=\mu x(t)(1-x(t))\]
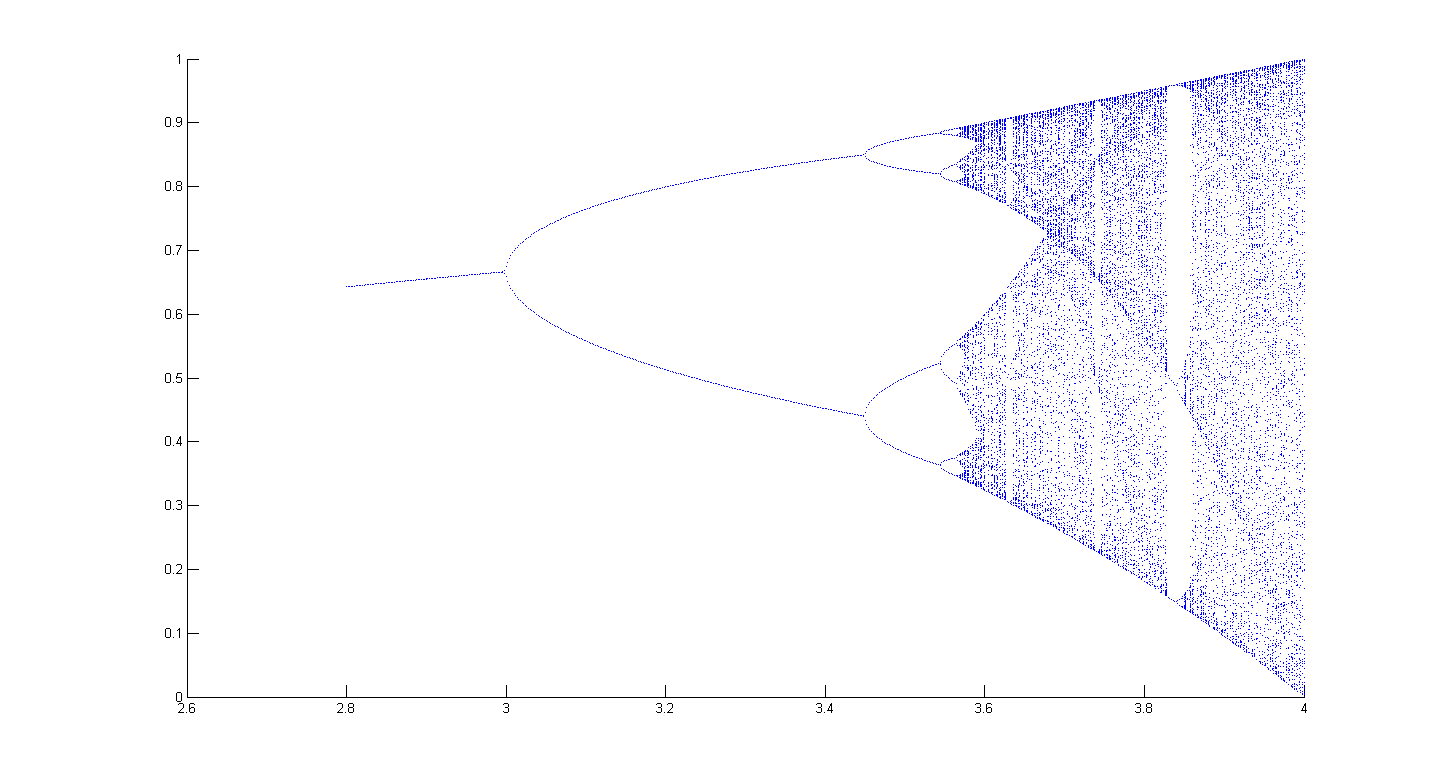
也是用于理解倍周期分岔的最基本、经典的模型。另外,除了用常规的相图来描述以外,还可以通过费根堡姆图来刻画其特性。具体就不细说了,当初做仿真的时候大概明白是什么原理,过了一段时间不用也就模糊了。
最后就是肖大大的“时空混沌扩频”PRL。不多说了……因为已经理解不能了。计算物理虽说没有理论物理那么复杂艰深,但对充分解释仿真结果能力的要求也很高……
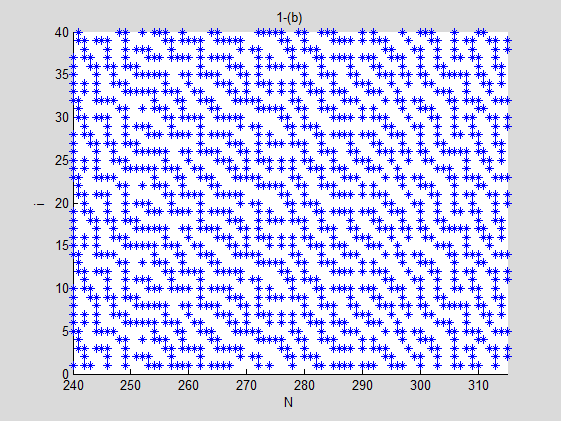
EMW related
动力学的东西很复杂,量子力学虽说课程简单但与前沿相去甚远,热力学和统计结合更是众说纷纭。搞来搞去,只有麦克斯韦方程组还在我理解范畴之内。其实表面位移电流已经有点超出我想象力了,但确实在一些情况下是能够合理解释现象的。整个四年学习,只有电磁波相关的内容我还能自始至终抓住主线。联系到工程中,最难的情况不过是两类贝塞尔函数,而计算机恰巧最擅长干解方程的事情了。
在实验中心并没有做太多的关于电磁的仿真,倒是光波导、电磁场与电磁波、光纤通信三门课程让我多方位地接触了电磁相关的分析方法。从常规的矩形波导圆波导,到平板波导和单模多模阶跃光纤,再到微结构和微腔,自己也算囫囵地了解了光电子方向的框架。简而言之,电磁波的分析和仿真无非就是对于各种各样不同边界条件的处理。因为波本身的传播已经让麦克斯韦老爷子一人包办了,后人只需要选择合适的波的种类,在合适的结构中寻找输入和输出的方法。当然,目前比较火的像光频梳,带隙导波等等则又是对波的更深的理解了。
说来说去,虽然理论上自己可以通过仿真解决很多问题,但真要动手操作可不是那么简单。简单仿真一个柱坐标的圆环磁场分布,都会写的磕磕绊绊,因为一是很难写对Biot-Savart在柱坐标系下的微分和积分(原谅我数学功底实在欠佳),二是在多维mesh下想不清楚到底需要取哪一维进行计算。总而言之,还是数学不给力,导致我的一切研究都困难重重。
如果以后能侥幸研究些东西,那我或许只能研究初等数学能解释的简单模型,或是利用人家的工具数值上仿真一些东西了……
不多说了,放图!
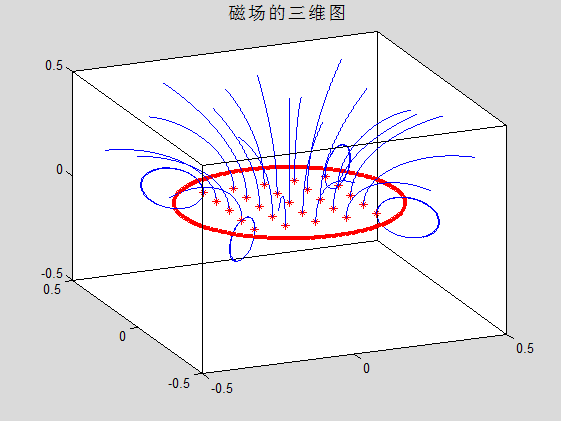
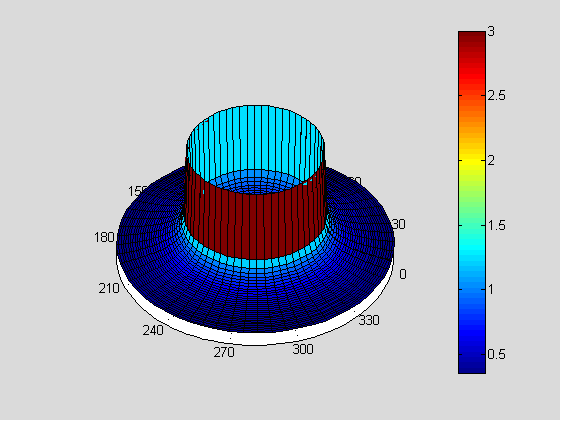
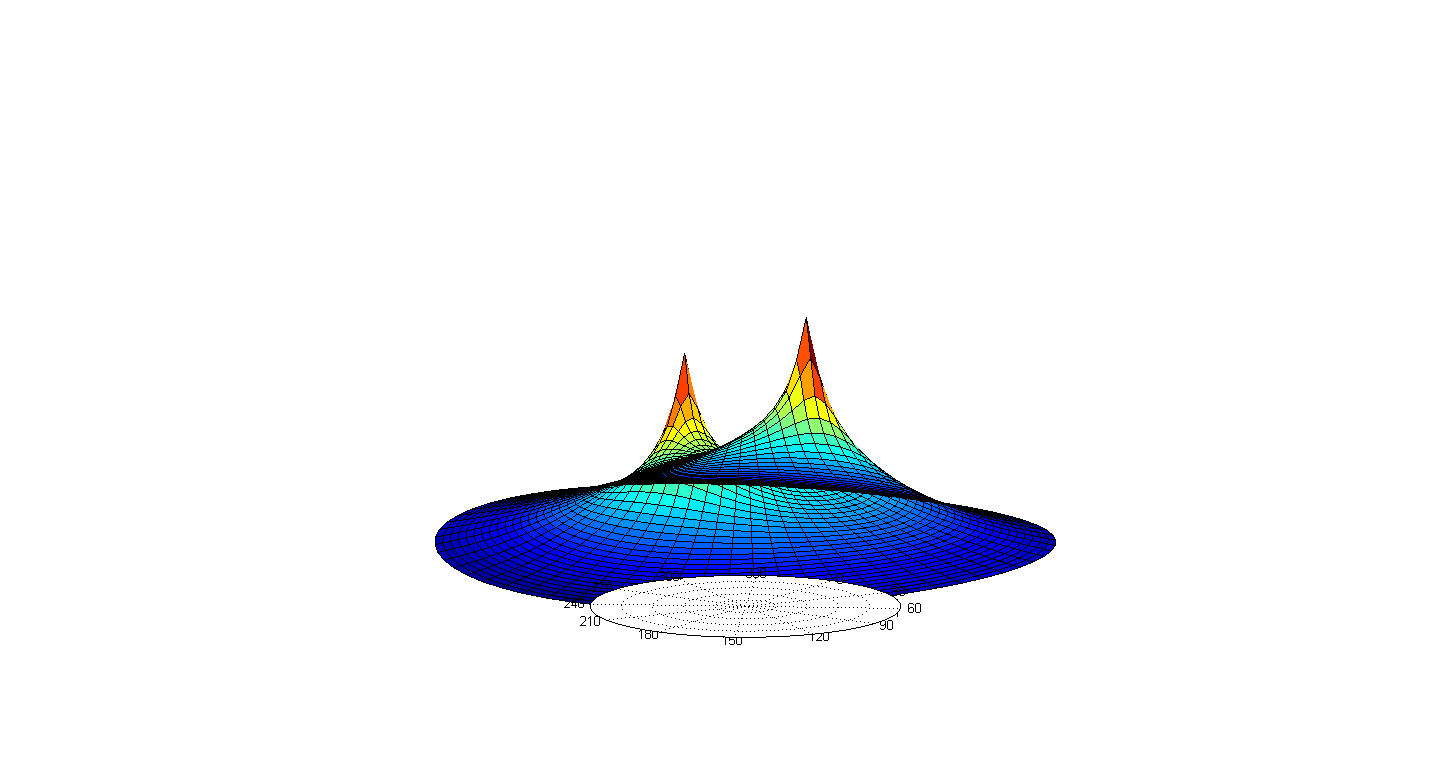
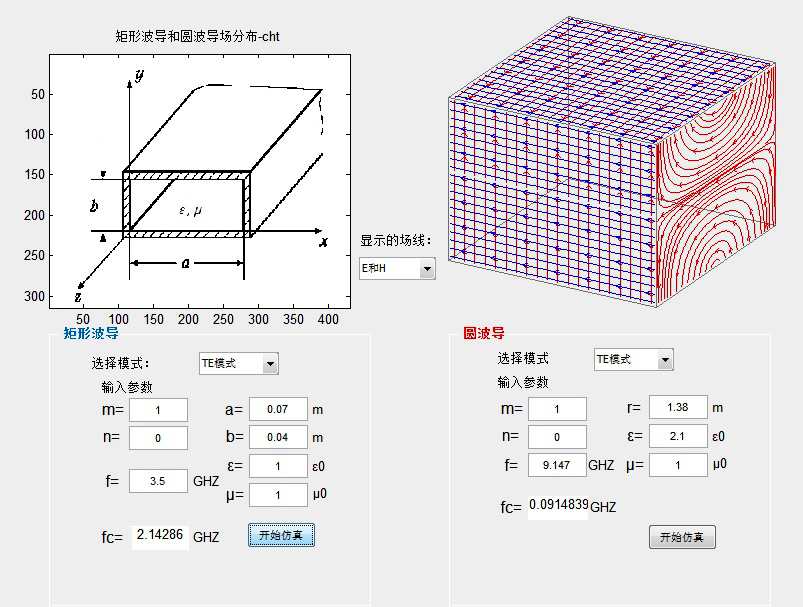
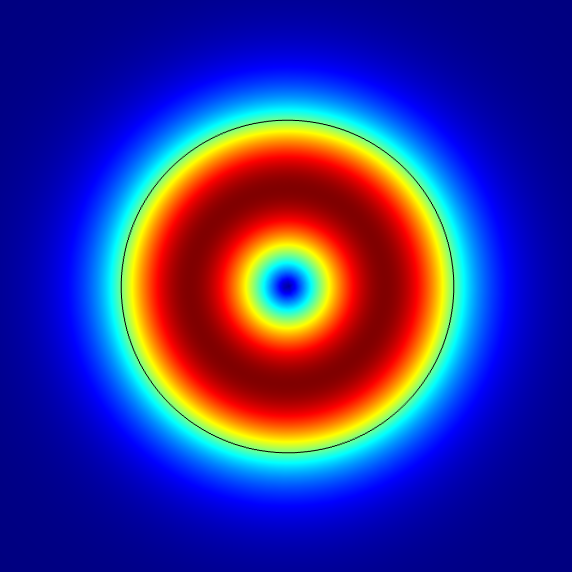
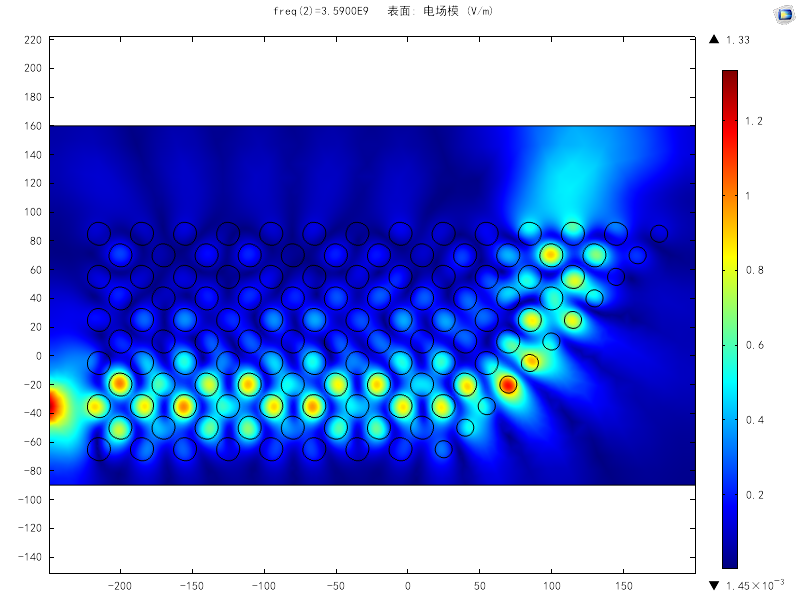

Others
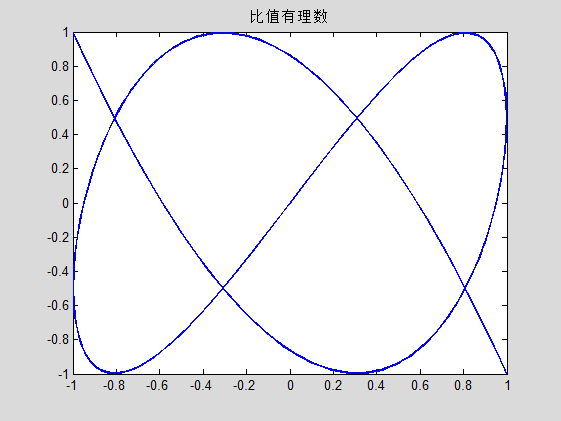
其实我真的很喜欢用程序来刻画各种现象。可惜能力不足,有时设计的模型与实际情况相去甚远。其实这一切的开始,都是源于第一次在示波器看到李萨如图形。那时感觉“哇好酷!”,于是就走上了仿真画图的不归路……
随便放几个其它门类的图像吧。也可以参考相册里GIF相关的内容。
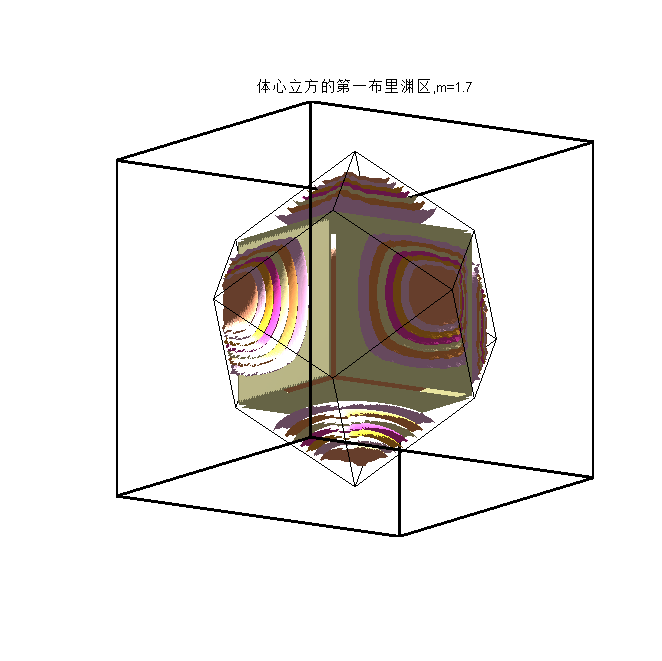
最后,关于振荡的内容,这是那个暑假花了好几个晚上补完的计算物理作业,诸君有兴趣可随意一看~
[^1]: Giordano N J, Nakanishi H. Computational physics : 2nd ed.[J]. 2011.
The previous duoshuo comment system stopped service. Please use disqus or submit issues to comment.